Category of elements

In category theory if C is a category and 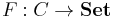$F: C \to \mathbf{Set}$ a set-valued functor the category of elements of F 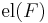$\mathop{\rm el}(F)$ (also denoted by ∫^CF) is the category defined as follows:

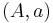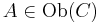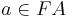Objects are pairs $(A,a)$ where $A \in \mathop{\rm Ob}(C)$ and $a \in FA$ .
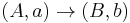An arrow $(A,a) \to (B,b)$ is an arrow 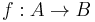$f: A \to B$ in C such that $(Ff)a = b$ .

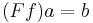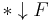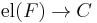A more concise way to state this is that the category of elements of F is the comma category $\ast\downarrow F$ where $\ast$ is a one-point set. The category of elements of F comes with a natural projection $\mathop{\rm el}(F) \to C$ that sends an object (A,a) to A and an arrow 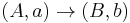$(A,a) \to (B,b)$ to its underlying arrow in C.

The Category of Elements of a Presheaf

Somewhat confusingly in some texts (e.g. Mac Lane, Moerdijk) the category of elements for a presheaf is defined differently. If 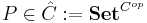$P \in\hat C�:= \mathbf{Set}^{C^{op}}$ is a presheaf the category of elements of P (again denoted by 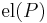$\mathop{\rm el}(P)$ or to make the distinction to the above definition clear ∫_C P) is the category defined as follows:

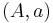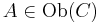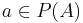Objects are pairs $(A,a)$ where $A \in \mathop{\rm Ob}(C)$ and $a\in P(A)$ .
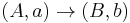An arrow $(A,a)\to (B,b)$ is an arrow 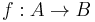$f:A\to B$ in C such that $(Pf)b = a$ .

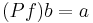As one sees the direction of the arrows is reversed and in fact one can once again state this definition in a more concise manner: the category we just defined is nothing but 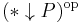$(\ast\downarrow P)^{\rm op}$ . Consequentially, in the spirit of adding a "co" in front of the name for a construction to denote its dual, one should rather call this category the category of coelements of P.

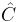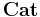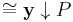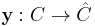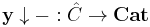For C small, this construction can be extended into a functor ∫_C from $\hat C$ to $\mathbf{Cat}$ , the category of small categories. In fact, using the Yoneda lemma one can show that ∫_CP $\cong \mathop{\textbf{y}}\downarrow P$ , where $\mathop{\textbf{y}}: C \to \hat{C}$ is the Yoneda embedding. This isomorphism is natural in P and thus the functor ∫_C is naturally isomorphic to $\mathop{\textbf{y}}\downarrow-: \hat C \to \textbf{Cat}$ .

References

Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics 5 (2nd ed.). Springer-Verlag. ISBN 0-387-98403-8.
Mac Lane, Saunders; Moerdijk, Ieke (1992). Sheaves in Geometry and Logic. Universitext (corrected ed.). Springer-Verlag. ISBN 0-387-97710-4.

External links

[1], definition and elementary properties of the category of elements in the nLab